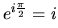
Physics Web recently asked its readers to nominate the world’s most beautiful equations. The winner? “Euler’s identity” equation, depicted above, which respondents variously described as “the most profound mathematical statement ever written”, “uncanny and sublime”, “filled with cosmic beauty”, and “mind-blowing”. What’s so cool about it? As Physics Web noted:

The equation contains nine basic concepts of mathematics — once and only once — in a single expression. These are [in order]: e (the base of natural logarithms); the exponent operation; pi; plus (or minus, depending on how you write it); multiplication; imaginary numbers; equals; one; and zero.

As one respondent noted, “What could be more mystical than an imaginary number interacting with real numbers to produce nothing?” Back in the 19th century, the American mathematician Benjamin Peirce gave a lecture proving “Euler’s identity”, and concluded:

“Gentlemen, that is surely true, it is absolutely paradoxical; we cannot understand it, and we don’t know what it means. But we have proved it, and therefore we know it must be the truth.”

Which is, of course, one of the great charms of hard-core mathematics and physics: If you frontload an equation into your brain that is complex enough, deep enough, and elegant enough, the sensation is pretty much indistinguishable from being baked out of your mind.

(Thanks to Slashdot for this one!)